Как создать идеальное дерево решений: для начинающих аналитиков данных и не только
Рассказываем, как правильно использовать дерево решений для машинного обучения, визуализации данных и наглядной демонстрации процесса принятия решений. Пригодится не только аналитикам данных, но и тем, кто хочет найти методику, помогающую более взвешенно принимать решения в жизни и бизнесе.
Основные задачи, которые дерево решений решает в машинном обучении, анализе данных и статистике:
- Классификация — когда нужно отнести объект к конкретной категории, учитывая его признаки.
- Регрессия — использование данных для прогнозирования количественного признака с учетом влияния других признаков.
Деревья решений также могут помочь визуализировать процесс принятия решения и сделать правильный выбор в ситуациях, когда результаты одного решения влияют на результаты следующих решений. Попробуем объяснить, как это работает на простых примерах из жизни.
Что такое дерево решений
Визуально дерево решений можно представить как карту возможных результатов из ряда взаимосвязанных выборов. Это помогает сопоставить возможные действия, основываясь на их стоимости (затратах), вероятности и выгоде.
Как понятно из названия, для этого используют модель принятия решений в виде дерева. Такие древовидные схемы могут быть полезны и в процессе обсуждения чего-либо, и для составления алгоритма, который математически определяет наилучший выбор.
Обычно дерево решений начинается с одного узла, который разветвляется на возможные результаты. Каждый из них продолжает схему и создает дополнительные узлы, которые продолжают развиваться по тому же признаку. Это придает модели древовидную форму.
В дереве решений могут быть три разных типа узлов:
- Decision nodes — узлы решения, они показывают решение, которое нужно принять.
- Chance nodes — вероятностные узлы, демонстрируют вероятность определенных результатов.
- End nodes — замыкающие узлы, показывают конечный результат пути решения.
Преимущества и недостатки методики дерева решений
Преимущества метода:
- Деревья решений создаются по понятным правилам, они просты в применении и интерпретации.
- Можно обрабатывать как непрерывные, так и качественные (дискретные) переменные.
- Можно работать с пропусками в данных, деревья решений позволяют заполнить пустое поле наиболее вероятным значением.
- Помогают определить, какие поля больше важны для прогнозирования или классификации.
Недостатки метода:
- Есть вероятность ошибок в задачах классификации с большим количеством классов и относительно небольшим числом примеров для обучения.
- Нестабильность процесса: изменение в одном узле может привести к построению совсем другого дерева, что связано с иерархичностью его структуры.
- Процесс «выращивания» дерева решений может быть довольно затратным с точки зрения вычислений, ведь в каждом узле каждый атрибут должен раскладываться до тех пор, пока не будет найден наилучший вариант решения или разветвления. В некоторых алгоритмах используются комбинации полей, в таком случае приходится искать оптимальную комбинацию по «весу» коэффициентов. Алгоритм отсечения (или «обрезки») также дорогостоящий, так как необходимо сформировать и сравнить большое количество потенциальных ветвей.
Как создать дерево решений
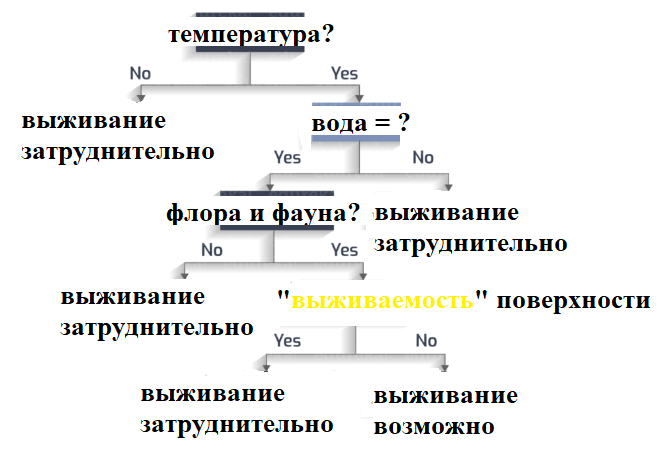
Для примера предлагаем сценарий, в котором группа астрономов изучает планету — нужно выяснить, сможет ли она стать новой Землей.
Существует N решающих факторов, которые нужно тщательно изучить, чтобы принять разумное решение. Этими факторами может быть наличие воды на планете, температурный диапазон, подвержена ли поверхность постоянным штормам, сможет ли выжить флора и фауна в этом климате и еще сотни других параметров.
Задачу будем исследовать через дерево решений.
- Пригодная для обитания температура находится в диапазоне от 0 до 100 градусов Цельсия?
- Есть ли там вода?
- Флора и фауна процветает?
- Подвержена ли поверхность планеты штормам?
Таким образом, у нас получилось завершенное дерево решений.
Правила классификации
Сначала определимся с терминами и их значениями.
Правила классификации — это случаи, в которых учитываются все сценарии, и каждому присваивается переменная класса.
Переменная класса — это конечный результат, к которому приводит наше решение. Переменная класса присваивается каждому конечному, или листовому, узлу.
Вот правила классификации из примера дерева решений про исследование новой планеты:
- Если температура не находится в диапазоне от -0,15 °C до 99,85 °C, то выживание затруднительно.
- Если температура находится в диапазоне от -0,15 °C до 99,85 °C, но нет воды, то выживание затруднительно.
- Если температура находится в диапазоне от -0,15 °C до 99,85 °C, есть вода, но нет флоры и фауны, то выживание затруднительно.
- Если температура находится в диапазоне от -0,15 °C до 99,85 °C, есть вода, есть флора и фауна, поверхность не подвержена штормам, то выживание возможно.
- Если температура находится в диапазоне от -0,15 °C до 99,85 °C, есть вода, есть флора и фауна, но поверхность подвержена штормам, то выживание затруднительно.
Почему сложно построить идеальное дерево решений
В структуре дерева решений выделяют следующие компоненты:
- Root Node, или корневой узел — тот, с которого начинается дерево, в нашем примере в качестве корня рассматривается фактор «температура».
- Internal Node, или внутренний узел — узлы с одним входящим и двумя или более исходящими соединениями.
- Leaf Node, или листовой узел — это заключительный элемент без исходящих соединений.
Когда создается дерево решений, мы начинаем от корневого узла, проверяем условия тестирования и присваиваем элемент управления одному из исходящих соединений. Затем снова тестируем условия и назначаем следующий узел. Чтобы считать дерево законченным, нужно все условия привести к листовому узлу (Leaf Node). Листовой узел будет содержать все метки класса, которые влияют на «за» и «против» в принятии решения.
Есть разные способы найти максимально подходящее дерево решений для конкретной ситуации. Ниже расскажем об одном из них.
Как использовать жадный алгоритм для построения дерева решений
Смысл подхода — принцип так называемой жадной максимизации прироста информации. Он основан на концепции эвристического решения проблем — делать оптимальный локальный выбор в каждом узле, так достигая решения, которое с высокой вероятностью будет самым оптимальным.
Упрощенно алгоритм можно объяснить так:
- На каждом узле выбирайте оптимальный способ проверки.
- После разбейте узел на все возможные результаты (внутренние узлы).
- Повторите шаги, пока все условия не приведут к конечным узлам.
Главный вопрос: «Как выбрать начальные условия для проверки?». Ответ заключается в значениях энтропии и прироста информации (информационном усилении). Рассказываем, что это и как они влияют на создание нашего дерева:
- Энтропия — в дереве решений это означает однородность. Если данные полностью однородны, она равна 0; в противном случае, если данные разделены (50-50%), энтропия равна 1. Проще этот термин можно объяснить так — это то, как много информации, значимой для принятия решения, мы не знаем.
- Прирост информации — величина обратная энтропии, чем выше прирост информации, тем меньше энтропия, меньше неучтенных данных и лучше решение.
Итого — мы выбираем атрибут, который имеет наибольший показатель прироста информации, чтобы пойти на следующий этап разделения. Это помогает выбрать лучшее решение на любом узле.
Смотрите на примере. У нас есть большое количество таких данных:
| Номер | Возраст (Age) | Уровень дохода (Income) | Студент (Student) | Кредитный рейтинг (CR) | Покупка компьютера (Buys Computer) |
| 1 | <30 | низкий (Low) | да | средний (Fair) | да |
| 2 | 30-40 | высокий (High) | нет | прекрасный (Excellent) | да |
| 3 | 40 | высокий (High) | нет | прекрасный (Excellent) | нет |
| 4 | <30 | средний (Medium) | нет | средний (Fair) | нет |
Здесь может быть n деревьев решений, которые формируются из этого набора атрибутов.
Ищем оптимальное решение с жадным алгоритмом
Первый шаг: создать два условных класса:
- «Да», человек может купить компьютер.
- «Нет», возможность отсутствует.
Второй шаг — вычислить значение вероятности для каждого из них.
- Для результата «Да», «buys_computer=yes», формула выглядит так:
- Для результата «Нет», «buys_computer=no», вот так:
Третий шаг: вычисляем значение энтропии, поместив значения вероятности в формулу.
Это довольно высокий показатель энтропии.
Четвертый шаг: углубляемся и считаем прирост информации для каждого случая, чтобы вычислить подходящий корневой атрибут для дерева решения.
Здесь нужно пояснение. Например, что будет означать показатель прироста информации, если за основу взять атрибут «Возраст»? Эти данные показывают, сколько людей, попадающих в определенную возрастную группу, покупают и не покупают продукт.
Допустим, среди людей в возрасте 30 лет и младше покупают (Да) два человека, не покупают (Нет) три человека. Info(D) рассчитывается для последних трех категорий людей — соответственно, Info(D) будем считать по сумме этих трех диапазонов значений возраста.
В итоге разница между общей энтропией Info(D) и энтропией для возраста Info(D) age (пусть она равна 0,694) будет нужным значением прироста информации. Вот формула:
Сравним показатели прироста информации для всех атрибутов:
- Возраст = 0,246.
- Доход = 0.029.
- Студент = 0,151.
- Кредитный рейтинг = 0,048.
Получается, что прирост информации для атрибута возраста является самым значимым — значит, стоит использовать его. Аналогично мы сравниваем прирост в информации при каждом разделении, чтобы выяснить, брать этот атрибут или нет.
Таким образом, оптимальное дерево выглядит так:
Правила классификации для этого дерева можно записать следующим образом:
- Если возраст человека меньше 30 лет и он не студент, то не будет покупать компьютер.
- Если возраст человека меньше 30 лет, и он студент, то купит компьютер.
- Если возраст человека составляет от 31 до 40 лет, он, скорее всего, купит компьютер.
- Если человек старше 40 лет и имеет отличный кредитный рейтинг, то не будет покупать компьютер.
- Если возраст человека превышает 40 лет, при среднем кредитном рейтинге он, вероятно, купит компьютер.
Вот мы и достигли оптимального дерева решений. Готово.